Оглавление
Логические задачи занимательной математики
№ I. Разминка
№ 1: Из Ленинграда в Москву надо передать почтой посылку в сундуке. Почта все ворует, если не заперто. Поэтому на этот сундук в Ленинграде вешается замок. Как передать посылку, чтобы на почте не украли и в Москве открыли? Задачка использовалась при отборе на малый мехмат МГУ.
№ 2: На какое наименьшее число процентов следует увеличить цену товара, чтобы, продавая его затем с 20%-ной скидкой от новой цены, не остаться в убытке, т. е. чтобы цена товара со скидкой была не меньше первоначальной?
№ 3: Носки считаются парой, если они имеют один цвет. Наугад из ящика с носками двух разных цветов выбирается три произвольных носка. Найдите вероятность того, что среди выбранных встретится хотя бы одна пара носков.
№ II. Логика
№ 4: Три деревни: Правдино (всегда говорят правду), Кривдино (всегда лгут) и Серединка — на — половинку (лгут через слово). Деревни находятся на равном расстоянии друг от друга, и друг друга не видят. Равноудаленно от каждой из них находится пожарная часть, из которой тоже не видно деревень. На пульт пожарному поступил звонок от жителя одной из деревень:
- «Пожар!».
- «Откуда звоните?»
- «Из Серединки на — половинку».
Вопрос: где пожар?
№ 5: Было три спорщика, ведущий и пять шляп: три черных и две белых. Ведущий завязал им глаза, и надел на каждого по шляпе. Когда спорщики открыли глаза, каждый видел только две шляпы на головах друзей, а свою не видел. Спорщики постояли немного, образовалась пауза…. и самый мудрый из них назвал цвет своей шляпы. Какого цвета были на них шляпы?
№ 6: Встречаются два человека, давно не виделись. Разговор заходит о детях.
- У тебя дети есть?
- Трое!
- А лет им по сколько?
- Ну, в сумме 13.
- А подробнее?
- Произведение возрастов соответствует числу окон в этом доме.
- Опять затрудняюсь.
- Старший из них рыжий.
- Ну, теперь все понятно!
Вопрос: по сколько им лет?
№ 7: Условие задачи выглядит следующим образом:
«Альберт и Бернард только что познакомились с Шерил и
захотели узнать, когда у нее день рождения. Шерил дала им список из десяти возможных дат:
- 15 мая, 16 мая, 19 мая;
- 17 июня, 18 июня;
- 14 июля, 16 июля;
- 14 августа, 15 августа, 17 августа.
Затем Шерил сообщила Альберту, в каком месяце она родилась, а Бернарду — какого числа. После этого между мужчинами произошел следующий разговор:
- Я не знаю, когда день рождения Шерил, но я знаю, что Бернард этого тоже не знает, — заявил Альберт.
- Сначала я не знал, когда у Шерил день рождения, но теперь знаю, — ответил Бернард.
- А теперь и я знаю, когда родилась Шерил, — сказал Альберт.
Так, когда же у Шерил день рождения?
№ 8: Школьник загадал два числа, оба строго больше единицы, такие, что сумма данных чисел меньше 99. Одному академику назвал их произведение, другому академику назвал их сумму.
Диалог академиков (начинает тот, кто знает сумму):
- Я понятия не имею, какое у вас произведение.
- Я знаю, что вы не знаете, какое у меня произведение.
- Теперь я знаю эти числа.
- Теперь и я их знаю.
Вопрос: какие это числа?
№ 9: На острове живет 25 человек: рыцари, лжецы и хитрецы. Рыцари всегда говорят правду, лжецы всегда лгут, а хитрецы отвечают на заданные им вопросы по очереди то правду, то ложь. Всем жителям острова было задано три вопроса: “Вы рыцарь?”, “Вы хитрец?”, “Вы лжец?”. На первый вопрос “Да” ответили 21 человек, на второй — 17 человек, на третий — 9 человек. Сколько хитрецов живет на этом острове?
№ 10: Во время Второй мировой войны командование американских и британских ВВС поручило математику Абрахаму Вальду выяснить, какие части фюзеляжа самолета нужно защитить дополнительной броней. При этом значительное увеличение брони снижало маневренность самолета. Вальд изучал самолеты, возвращавшиеся с боевых вылетов, отмечая места попаданий. В результате он рекомендовал установить дополнительную защиту на те участки (центральную и заднюю части фюзеляжа), где количество пробоин было минимальным. На каких выводах была основана его рекомендация?
№ 11: Каждый день больной должен принимать таблетки, чтобы не заболеть. По одной таблетке из каждой баночки. Иная дозировка — и можно отравиться. Баночки идентичные, таблетки — тоже. Оставалось 4 таблетки (по две каждого сорта), когда больной их случайно перемешал. Как можно закончить курс лечения и не отравиться?
№ 12: Загадка Эйнштейна. С одной стороны улицы подряд стоят пять домов, каждый своего цвета. В каждом живёт человек, все пять — разных национальностей. Каждый человек предпочитает уникальную марку сигарет, напиток и домашнее животное. Кроме того: Англичанин живёт в красном доме.
- Швед держит собаку.
- В зелёном доме пьют кофе.
- Датчанин предпочитает чай.
- Зелёный дом — по соседству слева от белого.
- Курильщик «Pall Mall» разводит птиц.
- В жёлтом доме курят «Dunhill».
- Молоко пьют в доме посередине.
- Норвежец живет в первом доме.
- Человек, курящий «Marlboro», живёт рядом с хозяином кошки.
- Дом, где курят «Dunhill», — рядом с тем, где держат лошадь. Любитель «Winfield» пьёт пиво.
- Немец курит «Rothmans».
- Норвежец живёт рядом с синим домом.
- Тот, кто курит «Marlboro», живет рядом с тем, кто пьет воду.
Вопрос:
- У кого живёт рыбка?
№ 13: Есть три урны с шарами. В каждой урне одна пара шаров. На урнах таблички ЧЧ, ББ, ЧБ. Соответственно Ч — черный шар, Б — белый. Таблички наклеены так, что ни одна из них не соответствует содержимому. Какое минимальное количество шаров нужно вынуть (вынимаем по одному шару из любой урны), чтобы можно было сказать, где какие пары шаров?
№ 14: Когда за доброе дело правитель страны решил наградить умного человека, тот пожелал взять столько золота, сколько весит слон. Но как же взвесить слона? В те времена не было таких весов. Что в подобной ситуации смогли бы придумать вы?
№ III. Теория вероятностей
№ 15: Пароход приходит к пристани между 13.00 и 14.00. Автобус отходит от пристани между 13.25 и 13.40. Пассажиру требуется 10 минут, чтобы перейти от парохода к остановке автобуса. Найти вероятность того, что он успеет на автобус.
№ 16: Вероятность того, что клиент банка не вернет кредит, в период экономического роста равна 0,04, а период экономического кризиса 0,13. Вероятность начала экономического кризиса оценивается в 0,35. Чему равна вероятность того, что клиент не вернет кредит?
№ 17: В денежной лотерее разыгрывается 1 выигрыш в 1 000 000 р., 10 выигрышей по 100 000 р. и 100 выигрышей по 1 000 р. при общем числе билетов 10 000. Найти справедливую цену одного лотерейного билета, т.е. такую цену, при которой лотерейная компания не получит ни прибыли ни убытка.
№ 18: Странное метро. У Виктора есть мама и невеста. Поезда в направлении к невесте Виктора приходят в 3.00, 3.10, 3.20 и т.д. А поезда к маме в 3.01, 3.11, 3.21 и т.д. Виктор приходит на вокзал в любое время с 3 до 5 и садиться в первый подошедший поезд. Какова вероятность, что Виктор поехал к невесте?
№ 19: Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти, первым или вторым, чтобы вероятность вынуть выученный билет была больше?
№ 20: Для приема зачета преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 по интегральному исчислению. Для сдачи зачета студент должен решить первую же доставшуюся наугад задачу. Какова вероятность для студента сдать зачет, если он умеет решить 17 задач по дифференциальному исчислению и 15 задач по интегральному исчислению?
№ 21: Идёт игра в русскую рулетку. В барабане револьвера шесть гнезд для патронов, в которые вставлено два патрона в соседние гнезда. Игрок вращает барабан и нажимает на спусковой крючок. Щелк! Повезло! Игроку необходимо еще раз нажать на крючок. Что ему лучше сделать: снова провернуть барабан или сразу нажать курок?
№ 22: Определить вероятность того, что в группе, состоящей из 23 человек, у двух людей будет совпадение дней рождения (число и месяц).
№ IV. Монеты
№ 23: Имеется 10 кучек с монетами, в каждой по 10 монет, в одной кучке все монеты фальшивые. Известно, что одна фальшивая монета весит на 1 гр. больше настоящей. Известен также вес настоящей монеты. За какое минимальное количество взвешиваний 12 можно определить в какой кучке фальшивые монеты? При этом весы могут быть любыми на ваш выбор.
№ 24: Известно, что среди 63 монет есть 7 фальшивых. Все фальшивые монеты весят одинаково, все настоящие монеты также весят одинаково, и фальшивая монета легче настоящей. Как за три взвешивания на чашечных весах без гирь определить 7 настоящих монет?
№ 25: Дана кучка из 100 монет. Ее требуется разбить на 100 кучек по одной монете в каждой, причем за шаг разрешается разбивать любую из имеющихся кучек монет на две непустые кучки. При этом если количество монет в двух кучках, получившихся при разбиении, различно, то оплачивается штраф в размере одного рубля, в противном случае штраф не платится. Какой наименьший штраф придется заплатить?
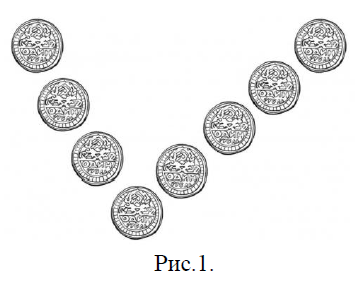
№ 26: Требуется переложить одну монету так, чтобы в обоих рядах было по пять монет (рис.1). Ряды должны оставаться прямыми.
№ V. Теория игр
№ 27: Пять пиратов на острове должны разделить между собой сотню золотых монет. Они делят добычу так: старший пират предлагает, как делить добычу, а потом каждый голосует, соглашаясь или нет. Если по меньшей мере половина пиратов проголосует «за», они поделят монеты, как предложил старший пират, если же нет, убивают старшего пирата и начинают все сначала. Самый старший пират (из тех кто выжил) предлагает новый план и т.д. до тех пор, пока какой-то план не будет принят. Какой план предложите Вы на месте старшего пирата? (Все пираты жадные, очень логичные и хотят жить).
№ 28: А, В и С сходятся для трехсторонней дуэли. Известно, что для А вероятность попасть в цель равна 0,3, для С — 0,5, а В стреляет без промаха. Дуэлянты могут стрелять в любого противника по выбору. Первым стреляет А, затем В, дальше С и т.д., пока лишь один человек останется жив. Какой должна быть стратегия А?
№ 29: Поле чудес. Три ящика. В одном ключи от автомобиля, в других самокаты. Ведущий знает, где что лежит. Допустим, вы выбираете какой-то ящик, например первый. Ведущий открывает другой ящик, допустим, третий. Там самокат. Вопрос: меняете ли вы свой выбор (в данном случае с первого на второй ящик) или нет. Ваш ответ?
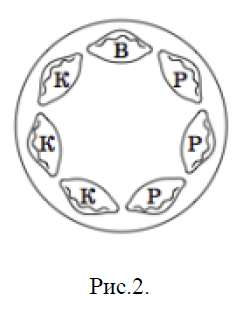
№ 30: Мама испекла пирожки — три с рисом, три с капустой и один с вишней — и выложила их на блюдо по кругу (см. рис.2). Потом поставила блюдо в микроволновку подогреть. На вид все пирожки одинаковые. Маша знает, как они лежали, но не знает, как повернулось блюдо. Она хочет съесть пирожок с вишней, а остальные считает невкусными. Как Маше наверняка добиться этого, надкусив как можно меньше невкусных пирожков?
№ 31: На доске записаны два числа: 2014 и 2015. Петя и Вася ходят по очереди, начинает Петя. За один ход можно либо уменьшить одно из чисел на его ненулевую цифру или на ненулевую цифру другого числа; либо разделить одно из чисел пополам, если оно четное. Выигрывает тот, кто первым напишет однозначное число. Кто из них может выиграть, как бы ни играл соперник? Опишите его стратегию и докажите, что она выигрышная.
№ 32: 300 гномов подошли к подвесному мосту, способному выдержать не более двух гномов одновременно. По мосту можно идти только с фонарём. Поодиночке они переходят мост в одну сторону за разное время: за 1, 2, …, 300 минут соответственно. Когда идут вдвоем, то движутся со скоростью более медленного. Каждый согласен пройти по мосту не более 3 раз (то есть, туда-обратно-туда). Фонарь только один. За какое наименьшее число минут они все смогут переправиться на другую сторону моста?
№ VI. Оптимальное управление
№ 33: Есть 100-этажный дом, испытатель и два стеклянных шара. Испытателю необходимо определить минимальное количество бросков, нужных для установления с какого конкретно этажа шар начинает разбиваться. Определить, сколько потребуется бросков.
№ 34: Определите размеры открытого бассейна объемом V = 32 м3, имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.
№ 35: Найти стороны треугольника, имеющего при данной площади S наименьший периметр.
№ VII. Задачи на движение
№ 36: Два поезда, находившиеся на расстоянии 200 км друг от друга, сближаются по одной колее, причем каждый развивает скорость 50 км/ч. С ветрового стекла одного локомотива в начальный момент движения взлетает муха и принимается летать со скоростью 75 км/ч вперед и назад между поездами, пока те, столкнувшись, не раздавят ее. Какое расстояние успевает пролететь муха до столкновения?
№ 37: Машина половину пути ехала со скоростью на 8 км/ч быстрее средней скорости, а вторую половину пути со скоростью в полтора раза меньшей средней. Определите среднюю скорость машины.
№ 38: Человек, рост которого 1,8 м, удаляется от источника света, находящегося на высоте 3 м., со скоростью 7,2 км/ч. С какой скоростью перемещается тень его головы?
№ 39: Автомобиль едет со скоростью 60 км/ч. С какой скоростью он должен ехать, чтобы каждый километр он проезжал на 1 минуту быстрее?
№ 40: Бизнесмен ехал на деловую встречу. Он рассчитывал, что если будет двигаться со скоростью 90 км/ч, то приедет на час раньше, а если 60 км/ч, то опоздает на час. С какой скоростью он должен ехать, чтобы не опоздать?
№ 41: Два автобуса ехали по шоссе со скоростью 60 км/ч, расстояние между ними было равно 600 метров. Начался (пологий) подъем, на котором скорость автобуса падает до 40 км/ч. Каким стало расстояние между автобусами, когда они оба находились на подъеме?
№ 42: Пункты A, B, C расположены последовательно, причем расстояние AB равно 3 км, а расстояние BC равно 4 км. Из пункта A выехал велосипедист и поехал в пункт С. Одновременно с ним из пункта B вышел пешеход и направился в пункт A. Известно, что пешеход и велосипедист пришли в пункты A и C одновременно. Найдите, на каком расстоянии от пункта A они встретились.
№ VIII. Экономические задачи
№ 43: Известно, что 10% человек владеют не менее, чем 90% всех денег в мире. Для какого наименьшего количества (в процентах) всех людей можно гарантировать, что эти люди владеют 95% всех денег?
№ 44: Жена отдала мужу сапоги и сказала: «Сходи, продай их за 25 рублей». Муж нашел двух одноногих калек и продал каждому по сапогу. Получилось так, что калеки скинулись по 12 с половиной руб. Когда Жена узнала, что сапоги муж продал калекам, попросила мужа отдать 5 рублей им обратно. По дороге Муж потратил 3 рубля, а оставшиеся 2 рубля отдал калекам (по рублю каждому). Получается что калеки потратили по 11 с половиной рублей (в сумме 23) и 3 рубля потратил муж. Значит сапоги стоили 23+3=26 рублей. Откуда взялся лишний рубль?
№ 45: У Незнайки и Пончика есть одинаковые суммы денег, составленные из монет достоинством 1, 3, 5 и 7 фертингов.
При этом у Незнайки 1 -фертинговых монет столько же, сколько у Пончика 3-фертинговых; 3-фертинговых — столько же, сколько у Пончика 5-фертинговых; 5-фертинговых — столько же, сколько у Пончика 7-фертинговых; а 7-фертинговых — столько же, сколько у Пончика 1 -фертинговых.
Определите, сколько 7-фертинговых монет у Незнайки, если известно, что у каждого — по 20 монет.
№ 46: Проводится лотерея. Предлагаются два конверта, в которых находятся две суммы денег, причём в одном из конвертов сумма отличается от суммы в другом конверте ровно в два раза. Никакие действия (измерительные и т. п.) совершать с конвертами нельзя. Можно лишь открыть один любой конверт и посчитать в нем деньги, после чего сделать выбор — взять этот конверт или взять другой конверт, чтобы получить большую сумму. Ваши действия?
№ 47: Учебник стоит число рублей, кратное 10. Первому школьнику не хватает 10 рублей для покупки учебника, второму — 20 рублей и так до десятого, которому не хватает 100 руб. Тогда они решили сложить деньги и купить хотя бы по одному учебнику на двоих. Но и тогда денег не хватило. Сколько стоит учебник?
№ 48: Задача Льюиса Керролла.
Счет перчаточному вору:
| Фунты | Шиллинги | Пенсы | |
| За похищенную перчатку | 2 | 0 | |
| За боль от потери | 3 | 8,5 | |
| За доставленное беспокойство | 4 | 4,5 | |
| За причинение неприятностей | 14 | 7 | |
| За потраченное время | 1 | 6 | |
| Итого: | 1 | 6 | 2 |
Зная, что в фунте больше шиллингов, чем в шиллинге пенсов, выясните, сколько в фунте шиллингов, а в шиллинге пенсов.
№ 49: Два вкладчика вложили деньги в общее дело. После этого один из них добавил еще 1 млн. рублей, в результате чего его доля в общем деле увеличилась на 0,04, а когда он добавил еще 1 млн., его доля увеличилась еще на 0,02. Сколько денег ему нужно добавить еще, чтобы увеличить свою долю еще на 0,04?
№ 50: Один торговец продаёт сливы по 150 рублей за килограмм, а второй — по 100 рублей. Но у первого косточка занимает треть веса каждой сливы, а у второго — половину. Чьи сливы выгоднее покупать?
№ 51: У Маши есть двухрублёвые и пятирублёвые монеты. Если она возьмёт все свои двухрублёвые монеты, ей не хватит 60 рублей, чтобы купить четыре пирожка. Если все пятирублёвые — не хватит 60 рублей на пять пирожков. А всего ей не хватает 60 рублей для покупки шести пирожков. Сколько стоит пирожок?
№ 52: Петин счет в банке составляет 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198. Какую максимальную сумму Петя может снять со счета, если других денег у него нет?
№ 53: Буратино увидел двух продавцов с красивыми книжками по одной цене. «Умненький Буратино, — зовет его один продавец — если ты купишь у меня две книжки, то я их обе продам тебе на 40% дешевле!». «Богатенький Буратино, — кричит другой, — если ты купишь у меня такую же книжку по обычной цене, то вторую я продам тебе всего за 20 сольдо!». Красавица Мальвина подсказала Буратино, что покупка двух книжек у первого продавца обойдется на 5 сольдо дешевле, чем у второго. Сколько стоила одна книжка сначала?
№ 54: Два человека варили кашу. Даниель дал для этого две меры крупы, а Леман — три меры. Когда каша была готова, подошел Пьер и попросил позволения съесть с ними кашу за плату. После еды он уплатил свою долю — 5 монет. Сколько денег причитается Леману?
№ 55: Не продешеви. Вас приглашают на работу финансовым аналитиком в крупную компанию, обещая начальную зарплату 100000 рублей в год и два варианта ее повышения: 1) Раз в год вам увеличивают зарплату на 15 000 р. 2) Раз в полгода — на 5 000 р. Какой вариант вам кажется выгоднее?
№ IX. Занимательные вычисления
№ 56: Найдите все двузначные числа, кратные произведению своих цифр.
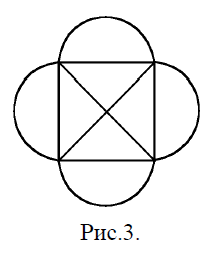
№ 57: Задачка по теории графов. Нарисовать данную фигуру (граф) не отрывая карандаша от бумаги и проводя каждое ребро (линию) только один раз (рис.3).
№ 58: Обнаружить неточности в следующей цепи рассуждений: интегрируя по частям в интеграле
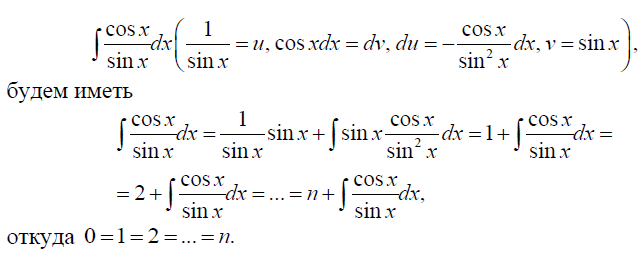
№ 59: На столе стоит 2014 коробок, в некоторых из них есть конфеты, а остальные пусты. На первой коробке написано: «Все коробки пустые». На второй — «По крайней мере 2013 коробок пустые». На третьей — «По крайней мере 2012 коробок пустые». На 2014-й — «По крайней мере одна коробка пустая». Известно, что надписи на пустых коробках ложны, а на коробках с конфетами — истинные. Определите, сколько коробок с конфетами.
№ 60: Сережа собирает игрушечные железные дороги. У него есть несколько наборов, в каждом из которых разное количество вагонов. Если все наборы объединить в один состав, то в нем будет 112 вагонов. Если взять три самых маленьких набора, то в них будет 25 вагонов, а в трех самых больших — 50 вагонов. Сколько наборов у Сережи? Сколько вагонов в самом большом наборе?
№ 61: Пин-код телефона состоит из 4 цифр (и может начинаться с нуля, например, 0951). Петя называет «счастливыми» такие пин- коды, у которых сумма крайних цифр равна сумме средних, например 1357: 1+7=3+5. В своем телефоне он использует только «счастливые» пин-коды. Петя говорит, что даже если забудет одну цифру (но будет помнить ее позицию), то он легко ее восстановит. А если он забудет две цифры (но будет помнить их позиции), то ему придется перебрать лишь небольшое количество пин-кодов. a) Сколько пин-кодов придется перебрать Пете в худшем случае? b) Сколько существует всего «счастливых» пин-кодов?
№ 62: Некоторое трехзначное число сложили с числом, записываемым теми же цифрами, но в обратном порядке, и получили 1777. Какие числа складывали?
№ 63: Различные числа х и у таковы, что X + 2015x = у2 + 2015у. Найдите х + у.
№ 64: Придумайте такое число АБВГ из четырех различных ненулевых цифр, чтобы оно делилось на трехзначное число БВГ, число БВГ делилось на двузначное число ВГ, а число ВГ делилось на Г.
№ 65: Некоторое четырехзначное число является точным квадратом. Если убрать первую цифру слева, то оно станет точным кубом, а если убрать 2 первые цифры, то оно станет четвертой степенью целого числа. Найдите это число.
№ 66: В ролевой игре «World of MSU» имеется три класса: воин, маг, целитель. Каждый игрок может управлять персонажем некоторого класса (одиночный класс) или персонажем, совмещающим способности двух классов (двойной класс), например, маг-целитель. Партия из 32 игроков штурмует «Цитадель зла». Известно, что целителей (т.е. всех, имеющих способности целителей) в два раза больше магов и в k раз меньше, чем воинов (k — целое число, большее двух). Сколько игроков имеют одиночный класс, если известно, что игроков, имеющих двойной класс на 2 больше, чем целителей?
№ 67: У отца есть три сына, родившихся в один и тот же день, но в разные годы. Младшему из сыновей 2 года. Через 12 лет возраст отца станет равен сумме возрастов его трех сыновей. Определите нынешний возраст среднего и старшего сыновей, если известно, что отцу сейчас 33 года.
№ 68: Позавчера Пете было 17 лет. В следующем году будет 20. Как такое может быть?
№ 69: Стопку листов формата А4 перегнули посередине и сложили в два раза (получилась брошюра формата А5). После этого перенумеровали страницы получившейся брошюры: 1, 2, 3, … Оказалось, что сумма чисел на одном из листов равна 74. Сколько листов было в стопке?
№ 70: В таблице 3×3 написаны следующие числа:
| 10 | 20 | 40 |
| 32 | 61 | 91 |
| 100 | 1000 | 2000 |
Разрешается за один ход менять местами любые два числа. За какое наименьшее количество ходов можно добиться того, чтобы сумма чисел в каждом столбце делилась на 3?
№ 71: Найдите количество чисел от 1 до 3400, кратных 34 и имеющих ровно 2 нечетных натуральных делителя. Например, само число 34 имеет делители 1, 2, 17 и 34, ровно два из которых нечетные.
№ 72: Известно, что дробь a/b меньше дроби c/d и b > d > 0. Определите, что меньше: среднее арифметическое этих двух дробей или дробь 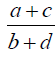 .
.
№ 73: Сказка про жадных медвежат. Два медвежонка нашли большую круглую головку сыра. Хотели поделить её поровну, но не сумели. Каждый боялся, что другому достанется больше. Вдруг откуда ни возьмись подошла к ним лиса. Давайте я вам поделю сыр поровну. Вот хорошо-то! — обрадовались медвежата. — Дели! Лиса взяла сыр и разломила его на две части, но так, что один кусок был больше другого. Медвежата закричали: Этот больше! Лиса успокоила их: Сейчас я всё улажу. Она откусила от большей части кусок, равный меньшей части. Теперь большим стал другой кусок. И так неровно! — забеспокоились медвежата. Ну, полно, — сказала лиса, — я сама знаю своё дело! И она снова откусила от большей кусок, равный меньшей части.
Лиса продолжала так делить сыр, пока не наелась. Всего она откусила по 3 раза от каждой части таким же образом — откусывая от одной части кусок, равный другой части. А медвежата только чёрными носами водили туда-сюда, туда-сюда: от большего куска — к меньшему, от меньшего — к большему. Но вот куски сравнялись, а медвежатам почти и сыра не осталось: два маленьких кусочка по 20 граммов каждый.
Ну что ж, — сказала лиса, — хоть и помалу, да зато поровну! Приятного вам аппетита, медвежата! — И, помахав хвостом, плутовка убежала.
Определите вес головки сыра, найденной медвежатами.
№ 74: Кое-кто в классе смотрит футбол, кое-кто — мультики, но нет таких, кто не смотрит ни то, ни другое. У любителей мультиков средний балл по математике меньше 4, у любителей футбола — тоже меньше 4. Может ли средний балл всего класса по математике быть больше 4?
№ 75: В некотором городе два района — старый и новый. Средняя высота зданий в старом районе вдвое меньше средней высоты зданий в новом районе и на 30% меньше, чем средняя высота зданий в городе. Найдите отношение количеств зданий в старом и новом районах.
№ 76: На выборах в городской совет за 7 партий было отдано 22410 голосов. Одна из партий получила больше голосов, чем каждая из остальных. Какое наименьшее число голосов она могла получить?
№ 77: В пруд пустили 30 щук, которые постепенно поедали друг друга. Щука считается сытой, если она съела трёх щук (сытых или голодных). Каково наибольшее число щук, которые могут насытиться?
№ 78: Задача Леонардо Пизанского (числа Фибоначчи). В место, огороженное со всех сторон стеной, поместили пару кроликов, природа которых такова, что любая пара кроликов производит на свет другую пару каждый месяц, начиная со второго месяца своего существования. Сколько пар кроликов будет через год?
№ 79: Четыре девочки поют песни, аккомпанируя друг другу. Каждый раз одна из них играет, а остальные поют. Оказалось, что
Анна спела меньше всех — пять. А Дороти — больше всех (восемь). Сколько всего песен спели девочки?
№ X. Занимательная геометрия
№ 80: Имеется 10 отрезков, длина каждого из которых выражается целым числом, не превосходящим 100. Приведите пример набора из 10 отрезков, такого, что ни из каких трех нельзя сложить треугольник.
№ 81: В таблице 3×4 надо расставить числа от 1 до 12 так, чтобы разность любых двух чисел, стоящих в одной строке была кратна 3, а разность любых двух чисел в одном столбце — кратна 4.
а) Сколькими способами это можно сделать? б) Можно ли расставить числа от 1 до 24 в таблице 6 х 4 так, чтобы разность любых двух чисел в одной строке была кратна 6, а разность любых двух чисел в одном столбце была кратна 4?
№ 82: Какое наименьшее количество клеток необходимо закрасить в квадрате 5 х 5 клеток, чтобы в любом квадрате 3 х 3 клетки было ровно 4 закрашенных клеток?
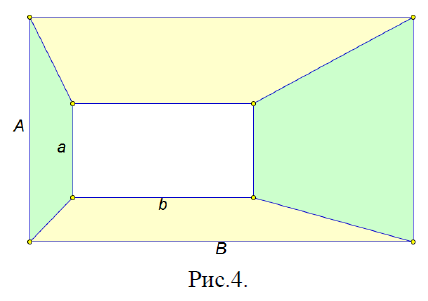
№ 83: Внутри большого прямоугольника размером А х В расположен маленький прямоугольник размером а х b (см. рис. 4). Найдите разность между суммарной площадью верхней и нижней трапеций и суммарной площадью боковых трапеций, если известно, что А = 20, В = 30, а = 4, b = 7.
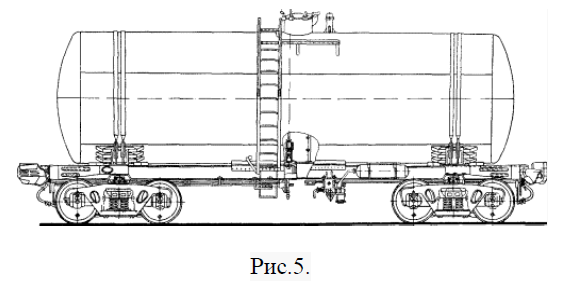
№ 84: Железнодорожная цистерна (рис. 5) заполнена бензином на 3/4 высоты. Поперечное сечение цистерны представляет собой эллипс с полуосями a = 2 и b = 1. Длина цистерны h=12, ширина 2a, высота 2b. Вычислить объем бензина в цистерне.
№XI. Фокусы с числами
№ 85: Предложите своему другу задумать какое-либо число. Затем заставьте его несколько раз поочередно умножать и делить задуманное им число на различные, произвольно вами назначаемые числа. Результат действий пусть он вам не сообщает. После нескольких умножений и делений остановитесь и предложите задумавшему число разделить полученный им результат на то число, которое он задумал, затем прибавить к последнему частному задуманное число и сказать вам результат. По этому результату вы немедленно угадываете число, задуманное вашим другом. Докажите этот арифметический фокус, т. е. покажите «на буквах», что фокус удается для любого задуманного числа.
№ 86: Фокусник попросил одного из зрителей написать на листе бумаги любое трехзначное число. Не показывайте мне — сказал фокусник, переедайте листок соседу. Я попрошу его приписать к числу справа такое же число и передать листок следующему зрителю. А он пусть разделить полученное шестизначное число на 13 и, не называя ответа, передаст листок следующему зрителю. Далее фокусник просит разделить полученное частное на 11. А что делать с остатком, спрашивает зритель. Остатка не будет, заверяет фокусник. И в самом деле, остатка не получилось. Следующего зрителя фокусник просит разделить полученное частное на 7, на отдельном листке написать последний результат и передать его фокуснику. Не заглядывая в листок, фокусник передает ее тому зрителю, который задумывал число: вот число которое вы написали. Верно! — удивляется зритель. Но откуда вы знаете? И в самом деле, откуда фокусник мог знать? Запишите и вы какое-нибудь трехзначное число и проделайте с ним все в описанном порядке.
№ 87: Тайна девятки. Существует множество других фокусов с числами, в которых используются некоторые любопытные особенности числа 9. Например, написав в обратном порядке любое трехзначное число (при условии, что первая и последняя цифры различны) и вычтя из большего числа меньшее, мы всегда получим в середине девятку и сумму крайних цифр, тоже равную 9. Это означает, что вы сразу можете назвать результат вычитания, зная только его первую или только последнюю цифру. Если теперь написать разность в обратном порядке и эти два числа сложить, то получится 1089.
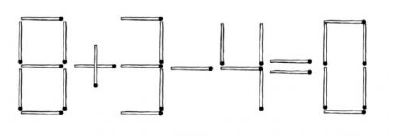
№ 88: Нужно переложить одну спичку так, чтобы получилось верное равенство. Задача хороша тем, что у нее есть четыре решения — одно жульническое, одно неточное и два правильных.
Парадоксы
Парадоксы можно найти везде, от экологии до геометрии и от логики до химии. Перед вами — восемь объяснений довольно увлекательных парадоксов. Некоторые из них настолько странные, что мы просто не можем полностью понять, в чём же суть.
Закон Бенфорда (закон первой цифры) (1)
Каков шанс, что случайное число начнётся с цифры «1»? Или с цифры «3»? Или с «7»? Если вы немного знакомы с теорией вероятности, то можете предположить, что вероятность — один к девяти, или около 11%.
Если же вы посмотрите на реальные цифры, то заметите, что «9» встречается гораздо реже, чем в 11% случаев. Также куда меньше цифр, чем ожидалось, начинается с «8», зато колоссальные 30% чисел начинаются с цифры «1». Эта парадоксальная картина проявляется во всевозможных реальных случаях, от количества населения до цен на акции и длины рек.
Физик Фрэнк Бенфорд впервые отметил это явление в 1938-м году. Он обнаружил, что частота появления цифры в качестве первой падает по мере того, как цифра увеличивается от одного до девяти. То есть «1» появляется в качестве первой цифры примерно в 30,1% случаев, «2» появляется около 17,6% случаев, «3» — примерно в 12,5%, и так далее до «9», выступающей в качестве первой цифры всего лишь в 4,6% случаев.
Чтобы понять это, представьте себе, что вы последовательно нумеруете лотерейные билеты. Когда вы пронумеровали билеты от одного до девяти, шанс любой цифры стать первой составляет 11,1%. Когда вы добавляете билет № 10, шанс случайного числа начаться с «1» возрастает до 18,2%. Вы добавляете билеты с № 11 по № 19, и шанс того, что номер билета начнётся с «1», продолжает расти, достигая максимума в 58%. Теперь вы добавляете билет № 20 и продолжаете нумеровать билеты. Шанс того, что число начнётся с «2», растёт, а вероятность того, что оно начнётся с «1», медленно падает.
Закон Бенфорда не распространяется на все случаи распределения чисел и псевдослучайные числа. Например, генератор случайных чисел, всевозможные лотереи, казино и наборы чисел, диапазон которых ограничен (человеческий рост или вес), под закон не попадают. Он также не работает с множествами, которые имеют только один или два порядка. Тем не менее, закон распространяется на многие типы данных. В результате власти могут использовать закон для выявления фактов мошенничества: когда предоставленная информация не следует закону Бенфорда, власти могут сделать вывод, что кто-то сфабриковал данные.
Парадокс Банаха-Тарского (2)
Представьте себе, что вы держите в руках шар. А теперь представьте, что вы начали рвать этот шар на куски, причём куски могут быть любой формы, какая вам нравится. После сложите кусочки вместе таким образом, чтобы у вас получилось два шара вместо одного. Каков будет размер этих шаров по сравнению с шаром-оригиналом?
Согласно теории множеств, два получившихся шара будут такого же размера и формы, как шар-оригинал. Кроме того, если учесть, что шары при этом имеют разный объём, то любой из шаров может быть преобразован в соответствии с другим. Это позволяет сделать вывод, что горошину можно разделить на шары размером с Солнце.
Хитрость парадокса заключается в том, что вы можете разорвать шары на куски любой формы. На практике сделать это невозможно — структура материала и в конечном итоге размер атомов накладывают некоторые ограничения.
Для того чтобы было действительно возможно разорвать шар так, как вам нравится, он должен содержать бесконечное число доступных нульмерных точек. Тогда шар из таких точек будет бесконечно плотным, и когда вы разорвёте его, формы кусков могут получиться настолько сложными, что не будут иметь определенного объёма. И вы можете собрать эти куски, каждый из которых содержит бесконечное число точек, в новый шар любого размера. Новый шар будет по-прежнему состоять из бесконечных точек, и оба шара будут одинаково бесконечно плотными.
Если вы попробуете воплотить идею на практике, то ничего не получится. Зато всё замечательно получается при работе с математическими сферами — безгранично делимыми числовыми множествами в трехмерном пространстве. Решённый парадокс называется теоремой Банаха-Тарского и играет огромную роль в математической теории множеств.
Бессмертный муравей на верёвке (3)
Представьте себе муравья, ползущего по резиновой верёвке длиной один метр со скоростью один сантиметр в секунду. Также представьте, что верёвка каждую секунду растягивается на один километр. Дойдёт ли муравей когда-нибудь до конца?
Логичным кажется то, что нормальный муравей на такое не способен, потому что скорость его движения намного ниже скорости, с которой растягивается верёвка. Тем не менее, в конечном итоге муравей доберётся до противоположного конца.
Когда муравей ещё даже не начал движение, перед ним лежит 100% верёвки. Через секунду верёвка стала значительно больше, но муравей тоже прошёл некоторое расстояние, и если считать в процентах, то расстояние, которое он должен пройти, уменьшилось — оно уже меньше 100%, пусть и ненамного.
Хотя верёвка постоянно растягивается, маленькое расстояние, пройденное муравьём, тоже становится больше. И, хотя в целом верёвка удлиняется с постоянной скоростью, путь муравья каждую секунду становится немного меньше. Муравей тоже всё время продолжает двигаться вперёд с постоянной скоростью. Таким образом, с каждой секундой расстояние, которое он уже прошёл, увеличивается, а то, которое он должен пройти — уменьшается. В процентах, само собой.
Существует одно условие, чтобы задача могла иметь решение: муравей должен быть бессмертным.
Парадокс экологического баланса (4)
Модель «хищник-жертва» — это уравнение, описывающее реальную экологическую обстановку. Например, модель может определить, насколько изменится численность лис и кроликов в лесу. Допустим, что травы, которой питаются кролики, в лесу становится всё больше. Можно предположить, что для кроликов такой исход благоприятен, потому что при обилии травы они будут хорошо размножаться и увеличивать численность.
Парадокс экологического баланса утверждает, что это не так: сначала численность кроликов действительно возрастёт, но рост популяции кроликов в закрытой среде (лесу) приведёт к росту популяции лисиц. Затем численность хищников увеличится настолько, что они уничтожат сначала всю добычу, а потом вымрут сами.
На практике этот парадокс не действует на большинство видов животных — хотя бы потому, что они не живут в закрытой среде, поэтому популяции животных стабильны. Кроме того, животные способны эволюционировать: например, в новых условиях у добычи появятся новые защитные механизмы.
Проблема настоящего времени (5)
Чтобы что-то могло физически существовать, оно должно присутствовать в нашем мире в течение какого-то времени. Не может быть объекта без длины, ширины и высоты, а также не может быть объекта без «продолжительности» — «мгновенный» объект, то есть тот, который не существует хотя бы какого-то количества времени, не существует вообще.
Согласно универсальному нигилизму, прошлое и будущее не занимают времени в настоящем. Кроме того, невозможно количественно определить длительность, которую мы называем «настоящим временем»: любое количество времени, которое вы назовёте «настоящим временем», можно разделить на части — прошлое, настоящее и будущее.
Если настоящее длится, допустим, секунду, то эту секунду можно разделить на три части: первая часть будет прошлым, вторая — настоящим, третья — будущим. Треть секунды, которую мы теперь называем настоящим, можно тоже разделить на три части. Наверняка идею вы уже поняли — так можно продолжать бесконечно.
Таким образом, настоящего на самом деле не существует, потому что оно не продолжается во времени. Универсальный нигилизм использует этот аргумент, чтобы доказать, что не существует вообще ничего.
Парадокс Моравека (6)
При решении проблем, требующих вдумчивого рассуждения, у
w /’~Ч w
людей случаются затруднения. С другой стороны, основные моторные и сенсорные функции вроде ходьбы не вызывают никаких затруднений вообще.
Но если говорить о компьютерах, всё наоборот: компьютерам очень легко решать сложнейшие логические задачи вроде разработки шахматной стратегии, но куда сложнее запрограммировать компьютер так, чтобы он смог ходить или воспроизводить человеческую речь. Это различие между естественным и искусственным интеллектом известно как парадокс Моравека. Ханс Моравек, научный сотрудник факультета робототехники Университета Карнеги-Меллона, объясняет это наблюдение через идею реверсного инжиниринга нашего собственного мозга. Реверсный инжиниринг труднее всего провести при задачах, которые люди выполняют бессознательно, например, двигательных функциях.
Поскольку абстрактное мышление стало частью человеческого поведения меньше 100 000 лет назад, наша способность решать абстрактные задачи является сознательной. Таким образом, для нас намного легче создать технологию, которая эмулирует такое поведение. С другой стороны, такие действия, как ходьба или разговор, мы не осмысливаем, так что заставить искусственный интеллект делать то же самое нам сложнее.
C-парадокс (7)
Гены содержат всю информацию, необходимую для создания и выживания организма. Само собой разумеется, что сложные организмы должны иметь самые сложные геномы, но это не соответствует истине.
Одноклеточные амёбы имеют геномы в 100 раз больше, чем у человека, на самом деле, у них едва ли не самые большие из известных геномов. А у очень похожих между собой видов геном может кардинально различаться. Эта странность известна как С- парадокс.
Интересный вывод из С-парадокса — геном может быть больше, чем это необходимо. Если все геномы в человеческой ДНК будут использоваться, то количество мутаций на поколение будет невероятно высоким.
Геномы многих сложных организмов включают в себя ДНК, которая ничего не кодирует. Это огромное количество неиспользованных ДНК, значительно варьирующееся от существа к существу, кажется, ни от чего не зависит, что и создаёт C-парадокс.
Эффект Мпембы (8)
Перед вами два стакана воды, совершенно одинаковые во всём, кроме одного: температура воды в левом стакане выше, чем в правом. Поместите оба стакана в морозилку. В каком стакане вода замёрзнет быстрее? Можно решить, что в правом, в котором вода изначально была холоднее, однако горячая вода замёрзнет быстрее, чем вода комнатной температуры.
Этот странный эффект назван в честь студента из Танзании, который наблюдал его в 1986-м году, когда замораживал молоко, чтобы сделать мороженое. Некоторые из величайших мыслителей — Аристотель, Фрэнсис Бэкон и Рене Декарт — и ранее отмечали это явление, но не были в состоянии объяснить его. Аристотель, например, выдвигал гипотезу, что какое-либо качество усиливается в среде, противоположной этому качеству.
Эффект Мпембы возможен благодаря нескольким факторам. Воды в стакане с горячей водой может быть меньше, так как часть её испарится, и в результате замёрзнуть должно меньшее количество воды. Также горячая вода содержит меньше газа, а значит, в такой воде легче возникнут конвекционные потоки, следовательно, замерзать ей будет проще.
Другая теория строится на том, что ослабевают химические связи, удерживающие молекулы воды вместе. Молекула воды состоит из двух атомов водорода, связанных с одним атомом кислорода. Когда вода нагревается, молекулы немного отодвигаются друг от друга, связь между ними ослабевает, и молекулы теряют немного энергии — это позволяет горячей воде остывать быстрее, чем холодной.
Ответы
- В Москве на этот сундук вешается еще один замок, затем отправляется обратно в Ленинград. Там снимается первый замок и сундук снова отправляется в Москву.
- 25%.
- 100%.
- Пожара нет.
- Черные.
- 9, 2 и 2.
- 16 июля.
- 4 и 13.
- 13.
- Исследовались самолеты, которые долетели до аэродрома.
- Разделить каждую таблетку пополам: одну половину положить в кучку для первого приема, а другую — для второго. Получим две кучки по 4 половины, и в каждой будет по 2 разного вида.
- У немца.
- Один шар из урны с табличкой ЧБ.
- Мудрец сделал так: он поместил слона в лодку, затем отметил по борту уровень воды. Когда слона вывели из лодки, осталось только поместить туда золото.
- 0,5.
- 0,0715.
- 210 р.
- 0,9.
- Не имеет значения.
- 0,64.
- Перед вторым выстрелом крутить барабан не надо.
- ≈ 50,73%.
- За одно взвешивание.
- 31+31+1, 15+15+1, 7+7+1.
- 2 рубля.
- Переложить верхнюю монету из правого ряда на самую нижнюю «стопкой».
- Пронумеруем пиратов от младшего к старшему. Вы пират №5. По одной монете дать номеру 1 и номеру 3. Остальные 98 оставить себе.
- Дуэлянту А при первом выстреле следует стрелять в воздух.
- Мнение нужно менять.
- Можно обойтись двумя надкусываниями.
- Выиграет Петя.
- 89699 минут.
- 14 бросков.
- Сторона бассейна 4 м, глубина 2 м.
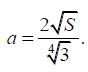
- 150 км.
- 8 км/ч.
- 5 м/с.
- Это невозможно.
- 72 км/ч.
- 400 м.
- 2,1 км.
- 55 %.
- 26 рублей составили расходы разных людей.
- 5 монет.
- Взять другой конверт.
- 100 рублей.
- В фунте 20 шиллингов, а в шиллинге 12 пенсов.
- 8 млн. руб.
- Выгоднее покупать по 100 рублей.
- 20 рублей.
- 498 долларов.
- 75 сольдо.
- 4 монеты.
- Второй вариант.
- 11, 12, 15, 24 и 36.
- Невозможно.
- Софизм. Забыли про константу.
- 1007 коробок.
- Два правильных варианта ответа: 9 наборов и 18 вагонов; 9 наборов и 19 вагонов.
- а) 10; b) 670.
- 839 и 938.
- — 2015.
- Например, 3125.
- 9216.
- 26 игроков.
- 3 года, 4 года.
- Если нынешний день 1 января, а День Рождения у Пети 31 декабря. Позавчера (30 декабря) ему было еще 17 лет, вчера (31 декабря) исполнилось 18 лет, в нынешнем году исполнится 19 лет, а в следующем году — 20 лет.
- 9 листов.
- 2 хода.
- 7.
- Дробь меньше.
- 680 г.
- Может.
- 4:3.
- 3203 голоса.
- 9 щук.
- 377 пар.
- 9 песен.
- 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. Данная последовательность называется последовательностью Фибоначчи.
- а) 144; б) Нет.
- 7 клеток.
- 20.
- ≈ 60,7.
- Секрет очень прост. Угадывающему самому тоже надо задумать произвольное число (например, 1) и проделывать над ним все назначаемые им умножения и деления вплоть до деления на первоначально задуманное число. Тогда в частном у него получится то же самое число, что и у другого задумавшего, хотя бы первоначально задуманные числа и были у них различными. После этого угадывающему надо вычесть из сообщенного ему результата свой результат. Разность и будет искомым числом. Пример. Задумано число 7. Умножено на 12. Результат (84) разделен на 2. Полученное число (42) умножено на 5. Результат (210) разделен на 3. Получилось 70, а после деления на задуманное число и прибавления задуманного числа —17. Одновременно вы «про себя» задумали число 1. Умножаете на 12 получается 12. Делите на 2, получается 6. Умножаете на 5, получается 30. Делите на 3, получается 10. Вычитая 10 из 17, получаете искомое число 7.
- Обратите внимание: во сколько раз шестизначное число больше первого трехзначного.
- Число 1089 пишется заранее на листе бумаги, который затем переворачивается лицевой стороной вниз. После того, как зритель окончит серию операций и объявит свой окончательный результат — 1089, покажите записанное вами предсказание, держа при этом лист вверх ногами. Написанное на нем число будет прочитано как 6801, что, конечно, не будет правильным ответом. Сделайте удивленное лицо, а затем извинитесь, что взяли лист не так, как нужно. Переверните его на 180 градусов и покажите верное число. Это небольшое попутное представление вносит развлекательный характер в демонстрацию фокуса.
- 9+3-4=8 правильное; 8+3-11=0 правильное; 6+3-9=0 неточное (девятка получается обрезанная); 8 — 3 — 4 ф 0 жульническое.








Добавить комментарий